|
|
 |
| HELE SHAW
|
 |
Bubble Raising Dynamics |
|
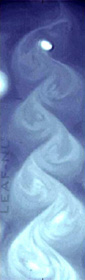
Viscous fluid flow between very close rigid walls obeys equations that mimic potential flow equations (Euler). Bubble raising in such cells provides an example of flow instabilities. The Hele-Shaw cell is an interesting set up to study simple Newtonian fluids and other complex fluids like gels, soft polymers and particle agregates. Two dimensional flow fields interacting with bluff bodies or alternatively, air bubbles rising at high velocities can set up the Bénard von Kármán (BvK) instability in a Hele-Shaw system. The instability marks the transition from a stationary wake flow to a periodic vortex shedding. In Hele-Shaw flows raising bubbles can exhibit a similar instability that is a periodic shedding of vortices (see left figure). Here a tracer (ink) introduced into the bubble path allows to visualize the periodic vortex emission. These vortices distort the bubble path periodically and we see a bubble in perfect oscillatory motion during the upward trip. We are working on these ideas as well as on the instability properties, like growth rate of most unstable modes and critical parameters for instability onset. |
|
The experimental set-up is shown in figure at right. A sandwich of two rigid plexiglass plates supported on a frame which allows to change the angle of the Hele-Shaw cell from 0 to 90 degrees and therefore the effect of gravity on the raising bubble. Pictures are captured with a rapid ccd camera. A laser ligth beam can be introduced across the cell in order to improve the quality of these images. Bubble injection is accomplished with screw-driven dosificator pushing air trough a syringe, to have an accurate control on the bubble size. |
|
|
|
|
|