|
|
|
THERMAL FLOWS |
 |
Rayleigh
Benard |
|
| |
Instabilities
in thermal non linear systems driven far from equilibrium, often
consist of transitions from motionless states to one varying
periodically in space or time. Popular examples are
Rayleigh-Bénard convection and thermal plumes. The onset of
periodic structures in these systems driven by spatially homogeneous or
time constant forcing, corresponds to a bifurcation characterized by
one or several modes that become unstable as a function of the forcing
mechanism. |
|
| |
 |
|
Rayleigh-Bénard (RB)
convection is a nonlinear problem where the velocity and temperature
are coupled. The onset of RB convection depends on the Rayleigh number
R and on the geometry of the container.
|
|
| For infinite parallel plates, there is a transition from
a pure
conductive regime to convection at the critical Rayleigh number R_c =
1708. The flow pattern consists of a series of counter rotating
infinite rolls with axes parallel to the thermal active walls in the
case of box-like containers, and concentric rolls in the case of
cylindrical-like containers. RB convection is an appropriate model to
understand the role of flow instabilities and laminar flow transitions.
The finite box problem is studied here experimentally usign high
Prandtl number fluids. |
|
|

|
| |
Our
convection cell is rectangular: 145mm long, 68mm deep and 23.5mm high.
The lateral walls are made of 10 mm thick Plexiglas, and top/bottom
plates are made of 16mm thick stainless steel. Several platinum sensors
(RTD-100) are placed in the two metal plate bodies, close to the cell
surface, to measure temperature gradient and uniformity. All
measurements are made with a Keithley 2000 multimeter and scan card in
4 wires configuration. |
|
|

|
The cold plate temperature is controlled with a
circulation from a
water bath, allowing better than 0.1K temperature uniformity and
stability. The other plate is heated with a 18W flat sheet resistance
of matched size. This resistance is connected to a DC power supply (HP
E3632A) in a 4 wires configuration, which allows precise heating power
setting. All instruments are remote controlled with a computer via GPIB
interface, which allows sampling temperature of the various sensors at
0.1 Hz and controlling hot temperature with a PID algorithm: we achieve
better than 0.5K temperature uniformity and 0.03K stability. |
| |
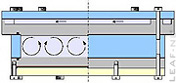
Convection rolls are shown in the figure at right. This front view of
the 6-roll pattern at low Rayleigh number in a high Prandtl number
fluid, was obtained using laser light illumination from the cell side.
The cell can be rotated along its short horizontal axis with a computer
controlled stepper motor to modify the orientation of the temperature
gradient and to study the effect of an external forcing over the
convection pattern. |
|
|
|
|
|
|
|