|
|
| |
NUMERICAL METHODS |
 |
Rayleigh Benard convection in 3D |
| |
Time dynamics of Rayleigh-Benard convection originating
from different heating rates for a Boussinesq fluid of Prandtl number
P=0.71 (Air) has been studied numerically inside a threedimensional
rectangular box where the height h (x) is 1/4 of the sides (y,z). The
heating rate, introduced through a time dependent Rayleigh number R(t),
drives a flow transition at least in the range of supercritical
Rayleigh numbers (R_s) here considered to solve the governing
equations; R_s = 3.6E3, 5E3, 9E3, 1.3E4 and 1.6E4. The flow transition,
identified by a change of the rotation sense of a two-roll fluid
pattern, was found when perfectly conducting side walls were used. This
kind of flow transition has been reported in recent experiments.
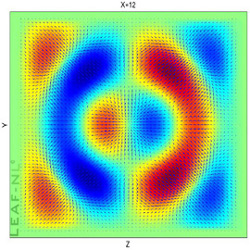
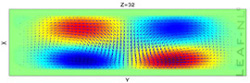
Figures below show the vector field at middle height from above and at
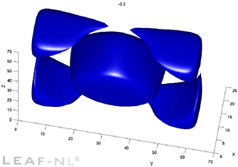
the cavity center from a side . Also shown is a 3D iso-surface of
vertical velocity distribution. |
| |
 |
 |
| |
|
| |
|
 |
Vortex dipoles in 2D |
| |
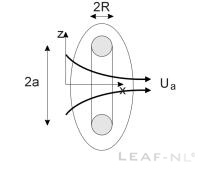
A vortex dipole of vortex pair is formed when we put two
individual vortices of opposite strength G
separated by a distance 2a in a fluid. Two Oseen-Lamb vortices will
have a self-induced velocity making the pair to move with self-induced
velocity Ua proportional to the individual strength and to the inverse
of the separation distance. Here we solve and study the evolution of a
vortex pair in a 2D situation using our numerical code based on the
SIMPLER method. We solve Navier Stokes equations with an initial flow
condition given by two localized Oseen-Lamb vortices described by a
velocity and vorticity fields as shown below, where R is the size of
the viscous core . |
 |
|
| |
|
| |
| The
flow is then calculated in time showing the pair moving from left to
right. It is possible using the block-off method for solid bodies to
insert a wall in the ring’s path and to observe the vortex
impigning on a wall as shown in the figure at right. The diople creates
a weak boundary layer on the wall during impact, which breaks into
satellite vortices. |
|
|
|
|
|